verlet积分算法简介及程序实现
Verlet算法是积分运动方程中最为普遍的方法,相对来说也比较简单。对于verlet算法详细的介绍,可以参考维基百科:Verlet integration .
Verlet算法简要介绍
1. 将 x(t+Δt) 和 x(t-Δt) 进行泰勒展开

2. 将以上两个表达式进行相加,得到位置表达式
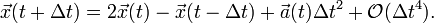
这个式子就显明,如果知道当前时刻的位置和加速度,前一时刻的位置,就可以推算出下一时刻的位置。
3. 将1中的两个式子相减,再同时除以 2Δt 即可获得速度表达式
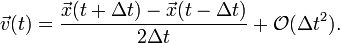
这个式子显明,只有在知道前一时刻和后一时刻的位置时,才有可能知道当前时刻的速度。也就是说,在当前时刻不能获得速度信息,必须要等到下一时刻的位置确定以后,才能返回来计算当前的速度。
4. 力(加速度)根据当前的位置 x(t),基于一定的势函数进行更新
Verlet算法积分步运行过程
要启动verlet算法,必须知道 t-2Δt 时刻和t-Δt 时刻的位置, t-2Δt 的速度和 t-Δt 时刻的加速度。具体演绎过程如下:
1. 根据 t-Δt 和 t-2Δt 时刻的位置、 t-Δt 时刻的加速度 ,获得当前时刻 t 的位置。
2. 根据当前时刻 t 的位置,更新当前位置下的加速度(受力)。
3. 同时,可以更新 t-Δt 时刻的速度。(速度是附带更新了,不更新速度并不妨碍积分过程继续下去。)
那么,现在就获得了t 时刻的位置, t-Δt 时刻的速度和 t 时刻的加速度,相当于将已知条件向前推进了一步(可以对比红色的部分)。
接下来的过程就是重复上面的过程。下图生动的反映了这个过程。

Verlet算法程序实现
下面以简谐振子为例给出Verlet算法的具体实现。下图为简谐振子示意图。

对于简谐振子,运动方程为:F = ma = -kx。
方程有解析解,为: x = Acos( wt + φ0) ,其中:
w = sqrt(k/m);
A = sqrt(x0*x0+v0*v0/(w*w));
φ0 = actan(-v0/(w*x0));
以上可以参考百度文库:简
给定初始条件为:k = 1, m = 1, r0 = 2, v0 = 2*sqrt(3).
则verlet算法的MATLAB实现如下:
function [r,v] = verlet(dt,totstep) % This script calculate the displacement, velocity, force % of harmonic ossication using verlet methods. % Input: % dt: timestep (recommend: 0.01 ~ 2.5) % totstep: total steps. % Powered By Xianbao Duan % Email: xianbao.d@gmail.com % Website: www.52souji.net %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % log: % 2012-06-05: Complete %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% % basic parameters k = 1; m = 1; r0 = 2; v0 = 2*sqrt(3); % verlet algorithm r(1) = r0; v(1) = v0; F(1) = -k*r(1); r(2) = r(1)+v(1)*dt+0.5*dt*dt*F(1)/m; F(2) = -k*r(2); for i = 2:totstep r(i+1) = 2*r(i)-r(i-1)+dt*dt*F(i)/m; v(i) = 0.5*(r(i+1)-r(i-1))/dt; F(i+1) = -k*r(i+1); end % delete the redundant elements r(end) = []; F(end) = [];
注:最后两行是将数组 r 和 v 赋空值,从而使得 r 和 v 的长度保持等于 totstep。
可以使用以下命令调用以上函数:
>> [r,v]=verlet(0.01,3000);
>> plot(1:3000,r)
>> grid on
>> xlabel('steps')
>> ylabel('displacement')
>> title('verlet algorithm, dt=0.01, totstep=3000')
>> figure
>> plot(r,v)
>> grid on;
>> xlabel('displacement');
>> ylabel('velocity')
>> title('verlet algorithm, dt=0.01, totstep=3000')下图是绘制得到的位置随着时间步的变化

下图是绘制得到的速度随着时间的变化

这是一个圆,它实际上反映了能量的守恒。
(例子来自 单斌 教授上课课件)


已有 3 条评论
不错,认真学习了
赞赞赞
excellent!